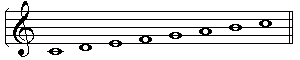Scale from scratch
- A scale is the set of notes belonging
to a key.
- Every scale has one of each note "name" in it:
- For example, a scale (major/minor of any type) that starts on a "C" say,
(whether the C is natural, sharp or flat) will have a "C", a "D", an "E", an "F",
a "G", an "A", a "B" and a "C" to finish. So, without any accidentals,
it will look like this:
However, a certain type of scale has specific gaps between each of the notes, so there
mat be some accidentals to add to this.
- A major scale always has the intervals TTSTTTS, where T=Tone, and S=Semitone,
or for some people, WWHWWWH where W=whole-step and H=Half-step.
- A melodic minor is WHWWWWH (up) and WWHWWHW (down)
- A harmonic minor is WHWWH3H (up and down), where 3=three half-steps
- Notice that each scale must end up on the same note it started on, so must consist
of a total of 12 half-steps within the seven intervals, so in most cases there
are two half-steps and the rest are whole-steps (the harmonic minor is the exception to this).
- You will also need to know that there is a Whole-step between each pair of adjacent notes except between E/F and B/C, which is only a half-step.
- So now you can work out, for example, that a scale of Dflat major has the notes DEFGABCD, but it starts on Dflat, so a W is Eflat, then a W is F, an H is Gflat, a W is Aflat, a W is Bflat, a W is C and an H to finish ends up back at Dflat
- How did the current scales we use come into being?
- The most basic scale is C major. This is the white notes on a piano going
from one C to another.
- Several questions arise immediately:
- Why are some notes on the piano white and some black, and why the pattern?
- Are there equal gaps between adjacent white notes, or black notes?
- How do you know where C is?
- Start with a note of any frequency (pitch).
- There are a number of other frequencies which
sound "similar" or "related" and which are also
mathematically related in their relative frequencies.
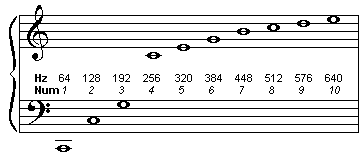
- For example, a note with double the frequency sounds very "similar" to
the first, and if they are sounded together you might have trouble
hearing them separately.
- If you blow across the top of a bottle, or blow a tube like a bugle or
hosepipe, there will be one "basic" note (called the fundamental frequency)
which is related to the length of the tube or volume of the bottle. If you
blow harder, you may well get another, higher, note, which sounds "related"
to the first. In fact, this is double the frequency of the first, and is
caused by the vibrations of half the length of the tube or bottle, rather
than the whole length, i.e. the wavelength is halved, so the frequency is
doubled.
- If you blow even harder (or in the case of a bugle, tighten your lips), you
may just hear another even higher note which will be the pipe or bottle
vibrating in thirds. So one-third of the wavelength, which means three
times the frequency.
- This process can be continued for some time, given the right circumstances,
and the pipe can be made to vibrate in four segments, five and so on.
You will notice that four times is double the original double, so the gap
between the first and second notes is the same as between the second and
the fourth, and the fourth and the eighth, and so on.
- If you take a piece of equipment which is able to play any frequency of
note (given the number of cycles per second), and take a fixed frequency,
let's say 100Hz, and play it. Then double the frequency to 200Hz and play
it. The sound will be higher than the first, but will have a quality
similar to the first sound. If we then play the two together, they will
sound quite reasonable, in fact it might be quite difficult to hear them
separately when they are played together - they seem to blend very well.
- So a basic scale came about by using notes derived from nature
Mail me
Copyright and disclaimer
Content and structure of these pages
Return to top